MATEMÁTICA FINANCEIRA

Conceitos básicos

    A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou financiamentos de bens de consumo. Consiste em empregar procedimentos matemáticos para simplificar a operação financeira a um Fluxo de Caixa.

    Capital

O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como: Principal, Valor Atual, Valor Presente ou Valor Aplicado. Em inglês usa-se Present Value (indicado pela tecla PV nas calculadoras financeiras).
 

    Juros

Juros representam a remuneração do Capital empregado em alguma atividade produtiva. Os juros podem ser capitalizados segundo dois regimes: simples ou compostos.   
   

JUROS SIMPLES: o juro de cada intervalo de tempo sempre é calculado sobre o capital inicial emprestado ou aplicado.JUROS COMPOSTOS: o juro de cada intervalo de tempo é calculado a partir do saldo no início de correspondente intervalo. Ou seja: o juro de cada intervalo de tempo é incorporado ao capital inicial e passa a render juros também.

  
    O juro é a remuneração pelo empréstimo do dinheiro. Ele existe porque a maioria das pessoas prefere o consumo imediato, e está disposta a pagar um preço por isto. Por outro lado, quem for capaz de esperar até possuir a quantia suficiente para adquirir seu desejo, e neste ínterim estiver disposta a emprestar esta quantia a alguém, menos paciente, deve ser recompensado por esta abstinência na proporção do tempo e risco, que a operação envolver. O tempo, o risco e a quantidade de dinheiro disponível no mercado para empréstimos definem qual deverá ser a remuneração, mais conhecida comotaxa de juros.

    Quando usamos juros simples e juros compostos?
    A maioria das operações envolvendo dinheiro utiliza juros compostos. Estão incluídas: compras a médio e longo prazo, compras com cartão de crédito, empréstimos bancários, as aplicações financeiras usuais como Caderneta de Poupança e aplicações em fundos de renda fixa, etc. Raramente encontramos uso para o regime de juros simples: é o caso das operações de curtíssimo prazo, e do processo de desconto simples de duplicatas.

    Taxa de juros

    A taxa de juros indica qual remuneração será paga ao dinheiro emprestado, para um determinado período. Ela vem normalmente expressa da forma percentual, em seguida da especificação do período de tempo a que se refere:

8 % a.a. - (a.a. significa ao ano).
10 % a.t. - (a.t. significa ao trimestre).

    Outra forma de apresentação da taxa de juros é a unitária, que é igual a taxa percentual dividida por 100, sem o símbolo %:

0,15 a.m. - (a.m. significa ao mês).
0,10 a.q. - (a.q. significa ao quadrimestre)

UROS SIMPLES


    O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal ou simplesmente principal é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos:



J = P . i . n



Onde:

J = juros P = principal (capital) i = taxa de juros n = número de períodos

   
    Exemplo: Temos uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m. pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que pagarei serão:
J = 1000 x 0.08 x 2 = 160
    Ao somarmos os juros ao valor principal temos o montante.
   Montante = Principal + Juros
   Montante = Principal + ( Principal x Taxa de juros x Número de períodos )



M = P . ( 1 + ( i . n ) )



    Exemplo: Calcule o montante resultante da aplicação de R$70.000,00 à taxa de 10,5% a.a. durante 145 dias.
    SOLUÇÃO:
    M = P . ( 1 + (i.n) )
    M = 70000 [1 + (10,5/100).(145/360)] = R$72.960,42
    Observe que expressamos a taxa i e o período n, na mesma unidade de tempo, ou seja, anos. Daí ter dividido 145 dias por 360, para obter o valor equivalente em anos, já que um ano comercial possui 360 dias.


---



   Exercícios sobre juros simples:
   1) Calcular os juros simples de R$ 1200,00 a 13 % a.t. por 4 meses e 15 dias.
    0.13 / 6 = 0.02167
    logo, 4m15d = 0.02167 x 9 = 0.195
    j = 1200 x 0.195 = 234


    2 - Calcular os juros simples produzidos por R$40.000,00, aplicados à taxa de 36% a.a., durante 125 dias.
    Temos: J = P.i.n
    A taxa de 36% a.a. equivale a 0,36/360 dias = 0,001 a.d.
    Agora, como a taxa e o período estão referidos à mesma unidade de tempo, ou seja, dias, poderemos calcular diretamente:
    J = 40000.0,001.125 = R$5000,00


    3 - Qual o capital que aplicado a juros simples de 1,2% a.m. rende R$3.500,00 de juros em 75 dias?
    Temos imediatamente: J = P.i.n ou seja: 3500 = P.(1,2/100).(75/30)
    Observe que expressamos a taxa i e o período n em relação à mesma unidade de tempo, ou seja, meses. Logo,
    3500 = P. 0,012 . 2,5 = P . 0,030; Daí, vem:
    P = 3500 / 0,030 = R$116.666,67


   4 - Se a taxa de uma aplicação é de 150% ao ano, quantos meses serão necessários para dobrar um capital aplicado através de capitalização simples?

   Objetivo: M = 2.P
    Dados: i = 150/100 = 1,5
    Fórmula: M = P (1 + i.n)
    Desenvolvimento:
2P = P (1 + 1,5 n) 2 = 1 + 1,5 n n = 2/3 ano = 8 meses
JUROS COMPOSTOS
    O regime de juros compostos é o mais comum no sistema financeiro e portanto, o mais útil para cálculos de problemas do dia-a-dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.


    Chamamos de capitalização o momento em que os juros são incorporados ao principal.


Após três meses de capitalização, temos:
    1º mês: M =P.(1 + i)
    2º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) 
    3º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) x (1 + i)
    Simplificando, obtemos a fórmula:
  

M = P . (1 +  i)n



    Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.
    Para calcularmos apenas os juros basta diminuir o principal do montante ao final do período:
  

J = M - P



    Exemplo:
   Calcule o montante de um capital de R$6.000,00, aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês.
  (use log 1,035=0,0149 e log 1,509=0,1788)
   Resolução:
   P = R$6.000,00
    t = 1 ano = 12 meses
    i = 3,5 % a.m. = 0,035
    M = ?
  
   Usando a fórmula M=P.(1+i)ⁿ, obtemos:
   M  =  6000.(1+0,035)¹²  =  6000. (1,035)¹²
    Fazendo  x = 1,035¹² e aplicando logaritmos, encontramos:
   log x = log 1,035¹²    =>   log x = 12 log 1,035    =>   log x = 0,1788    =>   x = 1,509
   Então  M = 6000.1,509 = 9054.
    Portanto o montante é R$9.054,00
Relação entre juros e progressões
    No regime de juros simples:
    M( n ) = P + n r P

    No regime de juros compostos:
    M( n ) = P . ( 1 + r ) ⁿ
    Portanto:
• num regime de capitalização a juros simples o saldo cresce em progressão aritmética
• num regime de capitalização a juros compostos o saldo cresce em progressão geométrica


TAXAS EQUIVALENTES
    Duas taxas i₁ e i₂ são equivalentes, se aplicadas ao mesmo Capital P durante o mesmo período de tempo, através de diferentes períodos de capitalização, produzem o mesmo montante final.
• Seja o capital P aplicado por um ano a uma taxa anual i_a .
• O montante M ao final do período de 1 ano será igual a M = P(1 + i _a )
• Consideremos agora, o mesmo capital P aplicado por 12 meses a uma taxa mensal i_m .
• O montante M’ ao final do período de 12 meses será igual a M’ = P(1 + i_m)¹² .
    Pela definição de taxas equivalentes vista acima, deveremos ter M = M’.
    Portanto, P(1 + i_a) = P(1 + i_m)¹²
    Daí concluímos que 1 + i_a = (1 + i_m)¹²
    Com esta fórmula podemos calcular a taxa anual equivalente a uma taxa mensal conhecida.
    Exemplos:
    1 - Qual a taxa anual equivalente a 8% ao semestre?
    Em um ano temos dois semestres, então teremos: 1 + i_a = (1 + i_s)²
    1 + i_a = 1,08²
    i_a = 0,1664 = 16,64% a.a.
   
    2 - Qual a taxa anual equivalente a 0,5% ao mês?
    1 + i_a = (1 + i_m)¹²
    1 + i_a = (1,005)¹²
    i_a = 0,0617 = 6,17% a.a.

TAXAS NOMINAIS
    A taxa nominal é quando o período de formação e incorporação dos juros ao Capital não coincide com aquele a que a taxa está referida. Alguns exemplos:
- 340% ao semestre com capitalização mensal.- 1150% ao ano com capitalização mensal.
- 300% ao ano com capitalização trimestral.
    Exemplo:
     Uma taxa de 15 % a.a., capitalização mensal, terá 16.08 % a.a. como taxa efetiva:
    15/12 = 1,25                    1,0125¹² = 1,1608



TAXAS EFETIVAS
    A taxa Efetiva é quando o período de formação e incorporação dos juros ao Capital coincide com aquele a que a taxa está referida. Alguns exemplos:
- 140% ao mês com capitalização mensal.
- 250% ao semestre com capitalização semestral.
- 1250% ao ano com capitalização anual.
    Taxa Real: é a taxa efetiva corrigida pela taxa inflacionária do período da operação.

FLUXO DE CAIXA
    O fluxo de caixa serve para demonstrar graficamente as transações financeiras em um período de tempo. O tempo é representado na horizontal dividido pelo número de períodos relevantes para análise. Asentradas ou recebimentos são representados por setas verticais apontadas para cima e as saídas oupagamentos são representados por setas verticais apontadas para baixo. Observe o gráfico abaixo:





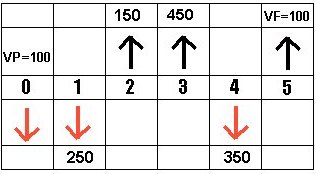
    Chamamos de VP o valor presente, que significa o valor que eu tenho na data 0; VF é o valor futuro, que será igual ao valor que terei no final do fluxo, após juros, entradas e saídas. 




VALOR PRESENTE e VALOR FUTURO
    Na fórmula M = P . (1 + i)ⁿ , o principal P é também conhecido como Valor Presente (PV = present value) e o montante M é também conhecido como Valor Futuro (FV = future value). 
    Então essa fórmula pode ser escrita como 
    FV = PV (1 + i) ⁿ 
    Isolando PV na fórmula temos:
    PV = FV / (1+i)ⁿ
    Na HP-12C, o valor presente é representado pela tecla PV.
    Com esta mesma fórmula podemos calcular o valor futuro a partir do valor presente.
    Exemplo:
    Quanto teremos daqui a 12 meses se aplicarmos R$1.500,00 a 2% ao mês?
    Solução:
         FV = 1500 . (1 + 0,02)¹² = R$ 1.902,36