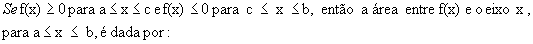
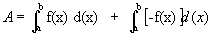 |
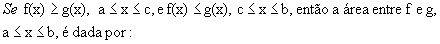
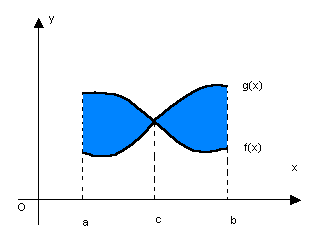
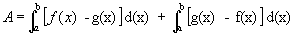 |
A integral definida, nos exemplos vistos, representa uma área, o que ocorre em muitos casos, e é uma das formas de se apresentar a integral definida.
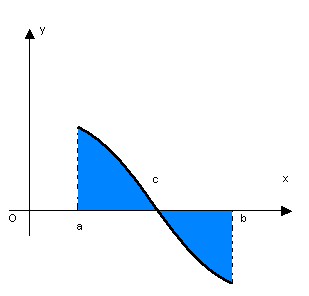
De forma geral, para  , a área limitada por f(x) e o eixo x,
, a área limitada por f(x) e o eixo x,  é dada por
é dada por 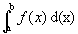 ,que pode representar a soma das áreas de infinitos retângulos de largura
,que pode representar a soma das áreas de infinitos retângulos de largura 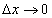 e cuja altura é o valor da função num ponto do intervalo da base:
e cuja altura é o valor da função num ponto do intervalo da base:
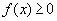 , a área limitada por f(x) e o eixo x,
, a área limitada por f(x) e o eixo x, 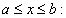 é dada por
é dada por 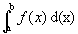 ,que pode representar a soma das áreas de infinitos retângulos de largura
,que pode representar a soma das áreas de infinitos retângulos de largura  e cuja altura é o valor da função num ponto do intervalo da base:
e cuja altura é o valor da função num ponto do intervalo da base: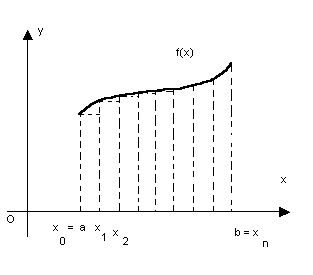
Subdividindo o intervalo [a, b] em n subintervalos através das abscissas x0=a, x1, x2,...,xn=b, obtemos os intervalos (a, x1), (x1, x2), ...., (xn-1, b). Em cada intervalo (xi-1, xi) tomemos um ponto arbitrário hi.
Seja  De acordo com a figura, os retângulos formados têm área
De acordo com a figura, os retângulos formados têm área 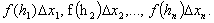
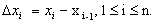 De acordo com a figura, os retângulos formados têm área
De acordo com a figura, os retângulos formados têm área 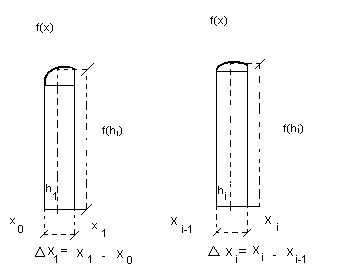
Então, a soma da áreas de todos os retângulos é:
que nos fornece um valor aproximado da área considerada.
Aumentando o número n de subintervalos 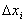 , tal que
, tal que 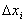 tenda a zero
tenda a zero 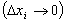 e o número n de subintervalos tenda a infinito
e o número n de subintervalos tenda a infinito 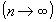 , temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
, temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
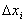 , tal que
, tal que 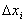 tenda a zero
tenda a zero 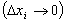 e o número n de subintervalos tenda a infinito
e o número n de subintervalos tenda a infinito 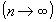 , temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
, temos as bases superiores dos retângulos e a curva praticamente se confundindo e, portanto, temos a área considerada.
Simbolicamente, escrevemos:
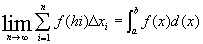 |
Exemplo:
Seja a área entre y = x e o eixo x, para 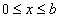 :
:
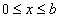 :
: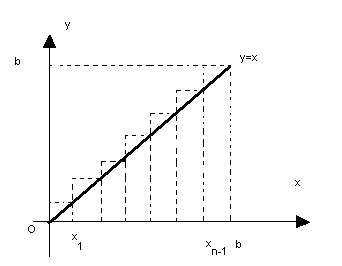
Esta área é dada por:
Podemos notar que o processo do limite nos leva ao resultado procurado. Dividindo o intervalo [0, b] em n subintervalos, cada um terá largura 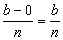 .
.
Sejam, então, os pontos 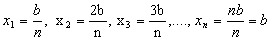 .
.
Como f(x) = x, então 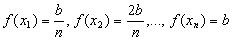 .
.
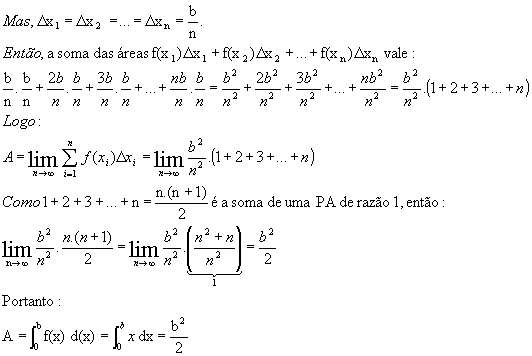
Nenhum comentário:
Postar um comentário