Em nosso dia-a-dia, vivemos cercados de máquinas. É muito comum nos depararmos com máquinas de todos os tipos, desde as mais simples até as mais complexas. Usamos um abridor para abrir latas, cortamos papel com uma tesoura, penduramos quadros em pregos fixados na parede pelos martelos e seguramos as crianças pequenas em carrinhos de bebê.
Somos cada vez mais dependentes de máquinas cada vez mais complexas, como os carros ônibus e os trens que utilizamos para ir a escola, ao local de trabalho etc.
Maquinas simples
Sabemos que as máquinas variam das mais simples as mais complexas. Máquinas complexas são aquelas que utilizam dispositivos eletrônicos em sua composição, como os circuitos integrados. Um exemplo de máquina complexa são os computadores.

Automóveis utilizam também recursos eletrônicos e elétricos, mas seu funcionamento se baseia principalmente em peças se deslocando: puxando, empurrando, girando etc.; enfim, são peças se movendo. Esse tipo de funcionamento, portanto, é do domínio da mecânica.
Toda máquina tem uma ou várias funções. Iremos iniciar o estudo de algumas maquinas que facilitam a atividade humana simplesmente por nos permitir realizar uma tarefa com menor esforço físico. Por exemplo, quando pregamos um prego na parede com um martelo, fazemos um esforço muito menor do que o necessário para pregá-lo usando apenas as mãos, o que certamente nem conseguiríamos.

Denominaremos de máquinas simples às que modificam e transmitem a ação de uma força para realizar algum movimento. Abridor de latas, martelo, tesoura, chave de fenda, alicate, quebra-nozes, carrinho de mão, pinça e cortador de unha são exemplos de máquinas simples.
Maquinas simples são aquelas que modificam e transmitem a ação de uma força para realizar algum movimento.
Alavancas
Imagine a seguinte situação: você precisa levantar um saco cheio de mantimentos. A massa total do saco é 120 kg. Poucas pessoas conseguem, e geralmente somente aquelas que se preparam para isso. Entretanto, no decorrer da história, as pessoas muitas vezes tiveram que levantar pedras ou objetos, e não contavam com máquinas para auxiliá-las. Há mais de 22 séculos, um homem chamado Arquimedes(287 – 212 a.C.) encontrou um método extremamente simples para resolver esse problema: ele descobriu as alavancas.
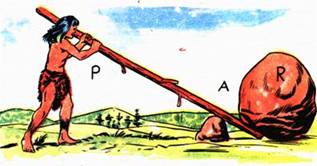
Uma alavanca nada mais é do que uma barra rígida que pode girar em torno de um ponto de apoio.
Em pleno século III a.C. Arquimedes afirmou: “Dê-me uma alavanca que moverei o mundo”
Como você poderia, com auxilio de uma alavanca, levantar um saco de 120 kg, fazendo uma força equivalente à que faria para levantar um saco de 20kg de arroz? Em outras palavras, como levantar uma massa com peso seis vezes maior que outra, fazendo a mesma força que faria para levantar essa?
Simples! É só a distância entre o ponto da barra rígida em que você aplica a força e o ponto de apoio (de P a A) ser seis vezes maior do que distância da massa até o ponto de apoio (de A a R).
Vamos denominar:
- Força resistente – é a força que queremos equilibrar. No exemplo acima, é o peso do saco de mantimentos.
- Força potente – é a força que sustentará a resistência. No exemplo, é a força que fazemos.
Tipos de alavancas
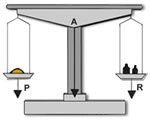
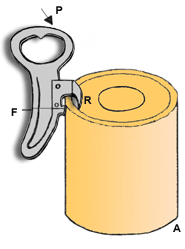
INTER-FIXA:
É quando o ponto apoio (A) está entre a aplicação da força potente (P) e a aplicação da força resistente (R).
|
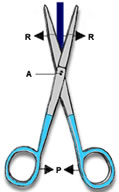
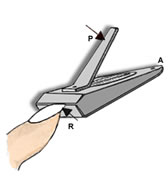
INTER-PONTENTE:
É quando a aplicação da força potente (P) está entre a aplicação da força resistente (R) e o ponto de apoio (A).
|
  | 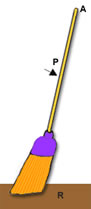  |
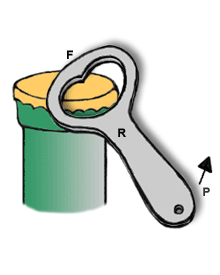
INTER-RESISTENTE:
É quando a aplicação da força resistente (R) está entre a aplicação da força potente (P) e o ponto de apoio (A).
|
  |
Equação das alavancas
Pediremos ajuda a matemática para encontrar uma expressão para a seguinte situação.
Equilibrar uma massa muito grande fazendo uma força bem menor que o peso dessa massa que queremos sustentar.
Vamos denominar:
R: valor da força resistente – a força que queremos equilibrar.
P: valor da força potente – é a força que sustentará a resistência.
BR: braço de resistência – é a distância do centro de gravidade do corpo ao ponto de apoio.
BP: braço de potência – é a distância do ponto de aplicação da força ao ponto de apoio.
O: Ponto de apoio
Verificamos que o equilíbrio será alcançado quando:
Exemplo de aplicação
Vamos calcular a força que um pedreiro tem de fazer para carregar 80 kg de terra com a ajuda de um carrinho de mão que possui 1,80 metros de comprimento. Sabendo que a distância entre o centro de gravidade do volume de terra até o centro da roda do carrinho é 90 cm.
Primeiramente vamos verificar qual tipo de alavanca temos.
Como o que fica no meio do carrinho é a terra, ou seja, a resistência, a alavanca é inter-resistente.
Temos:
braço de resistência = 90 cm = 0,9 m
braço de potência = 1,80 m
resistência = 80 kgf.
Portanto,
A interpretação física desse cálculo é a seguinte: o pedreiro necessita fazer uma força com intensidade de metade do peso do volume de terra para erguer o carrinho e transportar a carga.
Você percebeu a grande utilidade de uma máquina tão simples?
Nenhum comentário:
Postar um comentário