Dadas as retas r: a1x +b1y + c1 = 0 e s: a2x + b2y + c2 = 0, elas serão concorrentes se tiverem coeficientes angulares diferentes:
Como exemplo, vamos ver se as retas r: 3x - 2y + 1 = 0 e s: 6x + 4y + 3 = 0 são concorrentes:
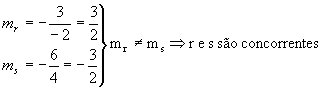
Perpendicularismo
Se r e s são duas retas não-verticais, então r é perpendicular a s se, e somente se, o produto de seus coeficientes angulares for igual a -1. Lê-se 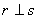 . Acompanhe o desenho:
. Acompanhe o desenho:
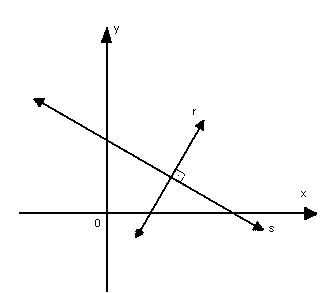
Ângulo entre duas retas
Sendo r e s duas retas não-verticais e não-perpendiculares entre si, pelo teorema do ângulo externo 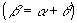 , temos:
, temos:
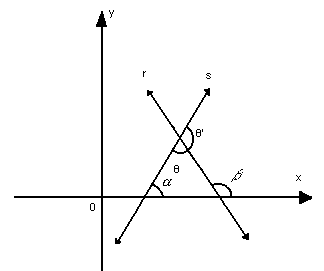
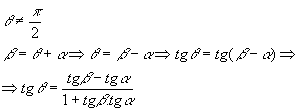
Dependendo da posição das duas retas no plano, o ângulo 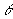 pode ser agudo ou obtuso. Logo:
pode ser agudo ou obtuso. Logo:
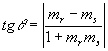
Essa relação nos fornece o ângulo agudo 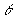 entre r e s, pois
entre r e s, pois 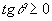 . O ângulo obtuso
. O ângulo obtuso 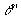 será o suplemento de
será o suplemento de 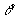 .
.
Distância entre ponto e reta
Dados um ponto P(x1, y1) e uma reta r:ax + by + c = 0, a distância entre eles (dpr)é dada por:
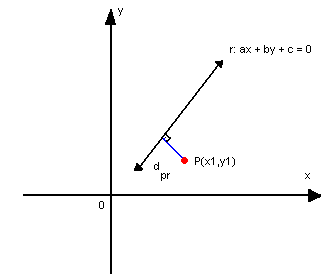 | 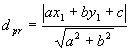 |
Vamos calcular a distância, por exemplo, do ponto P(-1,2) à reta r: x - 2y + 1 = 0.
Temos P(-1, 2) = P(x1, y1), a = 1, b= - 2 e c=1. Assim:
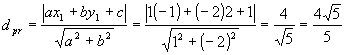
Bissetrizes
Dadas as retas concorrentes r: a1x + b1y + c1 = 0 e s: a2x + b2y + c2 = 0, o que se interceptam em um ponto Q, se P(x, y) é um ponto qualquer de uma das bissetrizes, P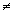 Q, então P equidista de r e s:
Q, então P equidista de r e s:
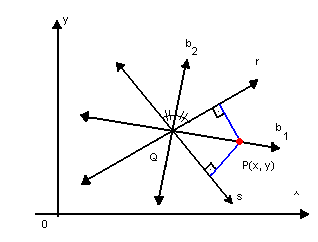
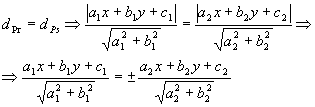
Considerando o sinal positivo, obtemos uma bissetriz; considerando o sinal negativo, obtemos a outra.
Vejamos um exemplo:
Se r: 3x + 2y - 7 = 0 e s: 2x - 3y + 1 = 0, então suas bissetrizes são:
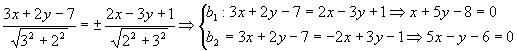
Nenhum comentário:
Postar um comentário