Cilindro, cone e esfera

Definições, área e volume:

1. Cilindro

Cilindro: Objeto tridimensional composto pela sobreposição de infinitos círculos de mesmo diâmetro. É também definido como o objeto que resulta da rotação de um paralelogramo em torno de um dos seus lados. Ou ainda, o cilindro pode ser visto como um "prisma" de base circular.

1.1 Cilindro reto: O cilindro é reto quando os círculos se sobrepõem ao longo de uma direção perpendicular ao plano dos mesmos. Ou quando o paralelogramo que executa a rotação é um retângulo. Neste caso o eixo do cilindro é perpendicular à sua base.
 

Definições complementares
A_l → área lateral
A_b → área da base
h → altura do cilindro (distância entre as duas bases e perpendicular a elas)
r → raio da base

Onde:
A_l = 2πrh A_b = πr²

Área total:
A_T = A_l + 2 . A_b = 2πrh + 2πr² = 2πr(h + r)

Volume:
V = A_b . h = πr²h

1.2 Cilindro oblíquo: quando o eixo o cilindro não é perpendicular à sua base.
 

As fórmulas para cálculo das áreas e do volume continuam as mesmas, pois a altura é sempre a distância entre as duas bases e perpendicular a elas ou ao plano que as contém.
 

2. Cone

Cone: Figura espacial que resulta da rotação de um triângulo em torno de um de seus lados. O cone pode ser considerado uma sobreposição de infinitos círculos com raios que decrescem até se reduzirem a um ponto. Pode ser visto também como uma "pirâmide" de base circular.

Cone reto: O cone é reto quando o triângulo que excuta a rotação é um triângulo retângulo girando em torno de um de seus catetos. O ponto fixo é chamado de vértice do cone, e sua distância até a base é a altura do cone.
 

Definições complementares

A_l → área lateral
A_b → área da base
h → altura do cone (distância entre a base, perpendicular a ela, e o vértice)
r → raio da base
s → geratriz do cone (segmento de reta que liga o vértice à circunferência da base)

Onde:

A_l = πrs
A_b = πr²

Área total:
A_T = A_l + A_b = πrs + πr² = πr (s + r)

Volume:

3. Tronco de cone

Tronco cone: É um objeto tridimensional que resulta do corte de um cone por um plano paralelo à base.
Quando o cone que sofre é o corte é um cone reto, temos um tronco de cone reto.
 

Definições complementares

A_l → área lateral
A_bm → área da base menor
A_bM → área da base maior
h → altura do tronco de cone (distância entre a base menor e a base maior e perpendicular a elas)
r → raio da base menor
R → raio da base maior
s → geratriz do cone (segmento de reta que liga o a circunferência da base menor à circunferência da base maior)

Onde:

A_bm = πr²
A_bM = πR²
A_l = πRs + πrs


Área total:
A_T = A_l + A_bM = πrs + πRs + πrs² = πr²

Volume:

4. Esfera

Esfera: É um objeto tridimensional que resulta da rotação de um círculo em torno de seu diâmetro.
 

r → raio da esfera


Área: A = 4πrs²

Volume:

4.1 Calota de esfera

Metaforicamente, a calota de uma esfera pode ser considerada como a "tampa de uma laranja".
 

r → raio da esfera
h → altura da calota

Área somente da calota:
A = 2πrh

Volume:

4.2. Fuso de uma esfera
Metaforicamente, o fuso de uma esfera pode ser considerado como a casca do "gomo de uma laranja".
 

r → raio da esfera
α → ângulo do fuso em graus

Área da lateral externa:

 

4.3. Cunha esférica
Metaforicamente, a cunha esférica pode ser considerada como o "gomo de uma laranja".

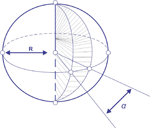r → raio da esfera
α → ângulo do fuso em graus

Volume: