Consideremos agora uma técnica chamada diferenciação logarítmica, a qual é útil para diferenciar funções compostas de produtos, de quocientes e de potências.
Exemplo
A derivada de
é relativamente difícil de ser calculada diretamente. Contudo, se primeiro tomarmos o logaritmo natural de ambos os lados e, então, usarmos suas propriedades, podemos escrever:
Diferenciando ambos os lados em relação a x, resulta
Assim, resolvendo para dy/dx e usando 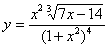obtemos
obtemos
OBSERVAÇÃO.Uma vez que 1n y é definido apenas para y > 0, a diferenciação logarítmica de y = f(x) é válida apenas nos intervalos onde f(x) for positiva. Assim, a derivada mostrada no exemplo é válida no intervalo ( 2, +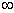
), uma vez que a função dada é positiva para x > 2. Contudo, a fórmula é realmente válida também no intervalo ( - , 2). Isso pode ser visto tomando-se valores absolutos antes de prosseguir com a diferenciação logarítmica e notando que 
está definido para todo y exceto em y = 0. Se fizermos isso e simplificarmos usando as propriedades de logaritmos e dos valores absolutos, obteremos
), uma vez que a função dada é positiva para x > 2. Contudo, a fórmula é realmente válida também no intervalo ( - 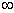, 2). Isso pode ser visto tomando-se valores absolutos antes de prosseguir com a diferenciação logarítmica e notando que 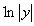está definido para todo y exceto em y = 0. Se fizermos isso e simplificarmos usando as propriedades de logaritmos e dos valores absolutos, obteremos
Diferenciando ambos os lados em relação a x dá lugar a , e, portanto, resulta em .Em geral, se a derivada de y = f(x) for obtida por diferenciação logarítmica, então a mesma fórmula para dy/dx resultará tomando-se ou não, primeiro, valores absolutos. Assim, uma fórmula da derivada obtida por diferenciação logarítmica será válida, exceto nos pontos onde f(x) for zero. A fórmula pode ser válida também naqueles pontos, mas não é garantido.
- DERIVADAS DAS FUNÇÕES EXPONENCIAIS
Para obter uma fórmula para a derivada de funções exponenciais
y =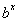 
reescrevemos esta equação como
x =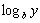 
e diferenciamos implicitamente usando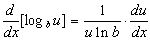 
para obter
para obter
que podemos reescrever usando y = 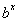como
como
Assim, mostrando que se 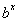for uma função diferenciável, então sua derivada em relação a x é
for uma função diferenciável, então sua derivada em relação a x é
No caso especial onde b = e temos 1n e = 1n, assim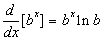 
torna-se
torna-se
Além disso, se u for uma função diferenciável de x, então tem-se a partir de 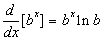e 
que
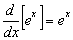e que
OBSERVAÇÃO.É importante distinguir entre diferenciar 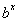(expoente variável e base constante) e 
(base variável e expoente constante).
(expoente variável e base constante) e 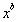(base variável e expoente constante).
Exemplo
Os cálculos a seguir usam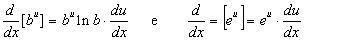 
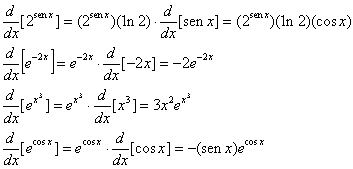
Nenhum comentário:
Postar um comentário