DOMÍNIO E IMAGEM DAS FUNÇÕES INVERSAS

• A equação seguinte

(f(x)) = x para todo x no domínio de f  f ((x)) = x para todo x no domínio de

implica em certas relações entre os domínios e as imagens de f e 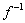. Por exemplo, na primeira equação a quantidade f (x) é uma entrada de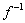, assim pontos nas imagens de f estão no domínio de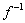; e na segunda equação, a quantidade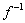(x)é uma entrada de f, sendo que pontos na imagem de  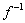estão no domínio de f. Tudo isso sugere as seguintes relações:

domínio de = imagem de f imagem de = domínio de f

Uma vez que f e g satisfazem duas condições:

• g(f(x)) = x para todo x no domínio de f
• f(g(y)) = y para todo y no domínio de g

concluímos que elas são inversas. Assim temos o seguinte resultado.

Se uma equação  y = f (x) pode ser resolvida para x como uma função de y, então ftem uma inversa e a equação resultante é x = (y)

• UM MÉTODO PARA ACHAR INVERSAS

Exemplo

Ache a inversa de f (x) =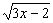 

Solução. Podemos achar uma fórmula para 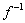(y) resolvendo a equação

y =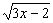 

para x como uma função de y. Os cálculos são:

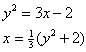
 da qual tem-se que 

Até aqui, fomos bem-sucedidos em obter uma fórmula para 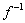; contudo não estamos realmente completos, uma vez que não há nenhuma garantia de que o domínio natural associado é o domínio completo para .

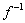Para determinar se isto é o que acontece, examinaremos a imagem de y = f (x) = 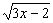. A imagem consiste de todos os y no intervalo 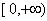, assim este intervalo é também o domínio de 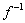(y); logo a inversa de f é dada  pela fórmula

OBSERVAÇÃO. Quando uma fórmula para 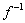 for obtida resolvendo-se a equação y = f(x) para x como uma função de y, a fórmula resultante tem y como a variável independente. Se for preferível ter x como a variável independente para 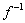, então há duas formas: você pode resolver y = f(x) para x com uma função de y, e então substituir y por x na fórmula final para  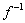, ou então você pode trocar x e y na equaçãooriginal  e resolver a equação x = f(y) para y em termos de x. Neste caso a equação final será y = 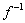(x).