GRÁFICO DAS FUNÇÕES INVERSAS

•        

O próximo objetivo é explorar as relações entre os gráficos de f e 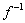. Com esse propósito, será desejável usar x como a variável independente para ambas as funções, o que significa estarmos comparando os gráficos de y = f(x) e y = 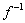(x).

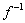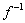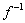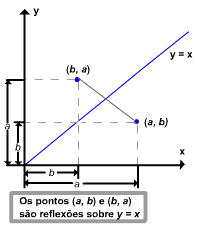
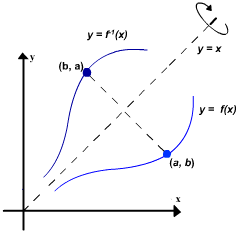
Se (a,b) for um ponto no gráfico y = f(x), então b = f(a). Isto é equivalente à afirmativa que a = (b), a qual significa que (b,a) é um ponto no gráfico de y = (x). Em resumo, inverter as coordenadas de um ponto no gráfico de f produz um ponto no gráfico de . Analogamente inverter as coordenadas de um ponto no gráfico de 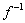 produz um ponto no gráfico de  f . Contudo, o efeito geométrico de inverter as coordenadas de um ponto é refletir aquele ponto sobre a reta y = x (figura 1), e logo os gráficos de y = f(x) e y = 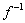(x) são um do outro em relação a esta reta (figura 2). Em resumo, temos o seguinte resultado.

Se f tiver uma inversa, então os gráficos de y = f(x) e y = (x) são reflexões um do outro em relação a reta y = x; isto é, cada um é a imagem especular do outro com relação àquela reta.

              

• FUNÇÕES CRESCENTES OU DECRESCENTES TÊM INVERSAS        

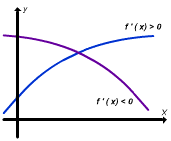
Se o gráfico da função f  for sempre crescente ou sempre decrescente sobre o domínio de f, então este gráfico pode ser cortado, no máximo, uma vez por qualquer reta horizontal e, conseqüentemente, a funçãof deve ter uma inversa. Uma forma de dizer se o gráfico de uma função é crescente ou decrescente em um intervalo é pelo exame das inclinações de suas retas tangentes. O gráfico de f deve ser crescente em qualquer intervalo, onde f'(x)>0 (uma vez que as retas tangentes têm inclinação positiva) e deve ser decrescente em qualquer intervalo onde f'(x)<0 (uma vez que as retas tangentes têm inclinação negativa). Essas observações sugerem o seguinte teorema.

Se o domínio de f  for um intervalo no qual f' (x)>0 ou no qual f'(x)<0, então a função f tem uma inversa.

Exemplo

O gráfico de f(x) = 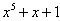 é sempre crescente em 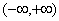, uma vez que

para todo x. Contudo, não há maneira fácil de resolver a equação y = 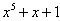 para x em termos de y; mesmo sabendo que f tem uma inversa, não podemos produzir uma fórmula para ela.

OBSERVAÇÃO. O que é importante entender aqui é que a nossa incapacidade de achar uma fórmula para a inversa não nega a sua existência; de fato, é necessário que se desenvolvam formas de achar propriedades de funções, as quais não têm fórmula explícita para se trabalhar com elas.