EXPOENTES IRRACIONAIS

Em álgebra, as potências inteiras e racionais de um número b estão definidas por

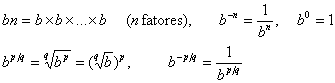
Se b for negativo, então algumas das potências fracionárias de b terão valores imaginários; por exemplo, 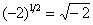. Para evitar esta complicação, vamos supor que 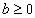, mesmo que não seja estabelecido explicitamente.

Observe que as definições precedentes não incluem potências irracionais de b, tais como

Há vários métodos para definir potências irracionais. Uma abordagem é definir potências irracionais de bcomo limite de potências racionais. Por exemplo, para definir 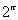 devemos começar com a representação decimal de 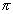, isto é,

3,1415926

Desta decimal, podemos formar uma seqüência de números racionais que ficam cada vez mais próximos de 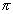   isto é,

3,1;   3,14;   3,141;   3,1415;   3,14159

e a partir destes podemos formar uma seqüência de potências racionais de 2:

Uma vez que os expoentes dos termos desta seqüência tendem a um limite 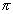, parece plausível que os próprios termos tendam a um limite; sendo assim, é razoável definir 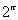como sendo este limite. A tabelaabaixo fornece evidência numérica de que a seqüência, na realidade, tem um limite e para quatro casas decimais, o valor deste limite é  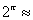8,8250. Em geral, para qualquer expoente irracional p e número positivo b, podemos definir 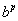como o limite de potências racionais de b, criadas pela expansão decimal de p.            

Tabela

x
3	8,000000
3,1	8,574188
3,14	8,815241
3,141	8,821353
3,1415	8,824411
3,14159	8,824962
3,141592	8,824974

• A FAMÍLIA DE FUNÇÕES EXPONENCIAIS

Uma função da forma f (x) = 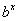, onde b > 0 e b 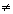1, é chamada de função exponencial de base b, cujos exemplos são 

f (x) = 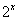,         f (x) = 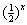,      f (x) =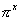  

Note que uma função exponencial tem uma base constante e um expoente variável. Assim as funções tais como f (x) = 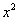 e  f (x) =  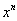não seriam classificadas como funções exponenciais, uma vez que elas tem uma base variável e um expoente constante.

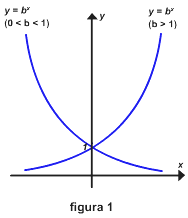
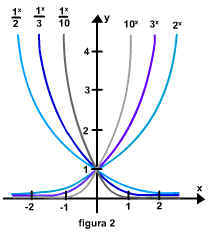
Pode ser mostrado que as funções exponenciais são contínuas e têm um dos dois aspectos básicos mostrados na figura 1, dependendo de se 0 < b < 1 ou b > 1. A figura 2 mostra os gráficos de algumas funções exponenciais específicas.

       

OBSERVAÇÃO. Se b = 1, então a função 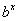 é constante, uma vez que 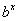=  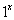= 1. Este caso não é de nosso interesse aqui, assim o excluímos da família das funções exponenciais.