1. 
2. 

3. 
4.
INTEGRAÇÃO POR PARTES
Dedução da Fórmula para a Integração por Partes
Se f e g são funções diferenciáveis, então, pela regra de diferenciação do produto,
Integrando ambos os lados, obtemos
ou
ou
Uma vez que a integral à direita irá produzir uma outra constante de integração, não há necessidade de manter o C nesta última equação; assim sendo, obtemos
(1)
|
a qual é chamada de fórmula de integração por partes. Usando esta fórmula, às vezes podemos tornar um problema de integração mais simples.
Na prática, é usual reescrever (1) fazendo
u=f(x), du=f '(x)dx
Isso dá lugar à seguinte forma alternativa para (1):
| (2) |
Exemplo
Calcule 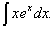
Solução. Para aplicar (2), precisamos escrever a integral na forma
Uma maneira de fazer isso é colocar
para que,
Deste modo,a partir de(2)
Nenhum comentário:
Postar um comentário