Para integrais definidas, a fórmula correspondente a (2) é:
Exemplo
Calcule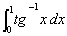
Solução. Seja
Assim,
Mas
logo
Fórmulas de Redução
A integração por partes pode ser usada para obter as fórmulas de redução para integrais. Estas fórmulas expressam uma integral com potência de função em termos de uma integral que envolve uma potência mais baixa daquela função. Por exemplo, se n for um inteiro positivo e n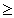 2, então a integração por partes pode ser usada para obter as fórmulas de redução.
2, então a integração por partes pode ser usada para obter as fórmulas de redução.
(2) 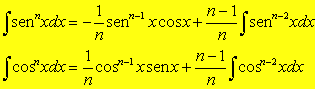
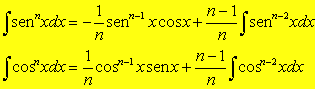
Para ilustrar como essas fórmulas são obtidas,vamos deduzir a fórmula (2).
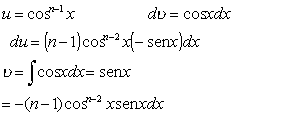
para que
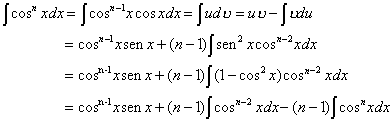
Transpondo o último termo para o lado esquerdo obtém-se
da qual tem-se(2).
Exemplo
Calcule 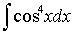
Solução. A partir de (2),com n=4
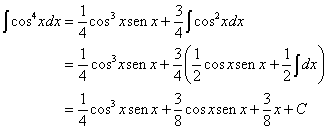
Nenhum comentário:
Postar um comentário