Entre os pontos de uma reta e os números reais existe uma correspondência biunívoca, isto é, a cada ponto de reta corresponde um único número real e vice-versa.
Considerando uma reta horizontal x, orientada da esquerda para direita (eixo), e determinando um pontoO dessa reta ( origem) e um segmento u, unitário e não-nulo, temos que dois números inteiros e consecutivos determinam sempre nesse eixo um segmento de reta de comprimento u:
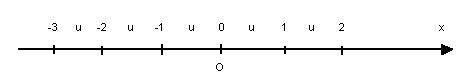
Medida algébrica de um segmento
Fazendo corresponder a dois pontos, A e B, do eixo x os números reais xA e xB , temos:

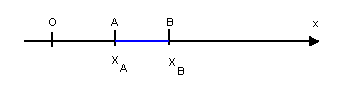
A medida algébrica de um segmento orientado é o número real que corresponde à diferença entre as abscissas da extremidade e da origem desse segmento.
Plano cartesiano
A geometria analítica teve como principal idealizador o filósofo francês René Descartes ( 1596-1650). Com o auxílio de um sistema de eixos associados a um plano, ele faz corresponder a cada ponto do plano um par ordenado e vice-versa.
Quando os eixos desse sistemas são perpendiculares na origem, essa correspondência determina um sistema cartesiano ortogonal ( ou plano cartesiano). Assim, há uma reciprocidade entre o estudo da geometria ( ponto, reta, circunferência) e da Álgebra ( relações, equações etc.), podendo-se representar graficamente relações algébricas e expressar algebricamente representações gráficas.
Observe o plano cartesiano nos quadros quadrantes:
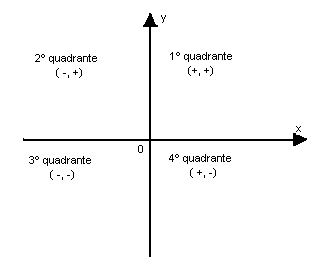

Exemplos:
- A(2, 4) pertence ao 1º quadrante (xA > 0 e yA > 0)
- B(-3, -5) pertence ao 3º quadrante ( xB < 0 e yB < 0)
Observação: Por convenção, os pontos localizados sobre os eixos não estão em nenhum quadrante.
Distância entre dois pontos
Dados os pontos A(xA, yA) e B(xB, yB) e sendo dAB a distância entre eles, temos:
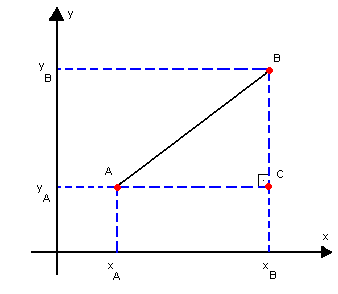 |
Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem:
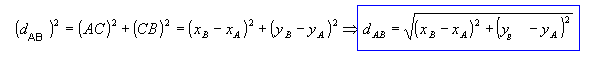
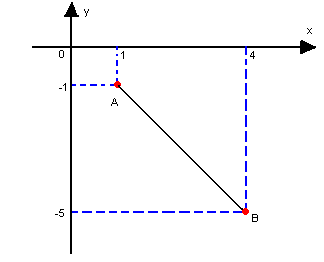
Como exemplo, vamos determinar a distância entre os pontos A(1, -1) e B(4, -5):
Nenhum comentário:
Postar um comentário