Geometria Analítica - Cônicas Elementos

   Observe a parábola representada a seguir. Nela, temos os seguintes elementos:

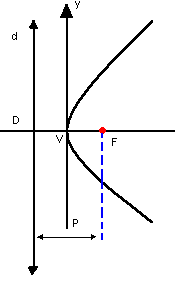
• foco: o ponto F
• diretriz: a reta d
• vértice: o ponto V
• parâmetro: p

                Então, temos que:

• o vértice V e o foco F ficam numa mesma reta, o eixo de simetria e.

                Assim, sempre temos .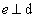

• DF =p
• V é o ponto médio de 

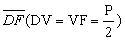
Equações

   Vamos considerar os seguintes casos:

a) parábola com vértice na origem, concavidade para a direita e eixo de simetria horizontal

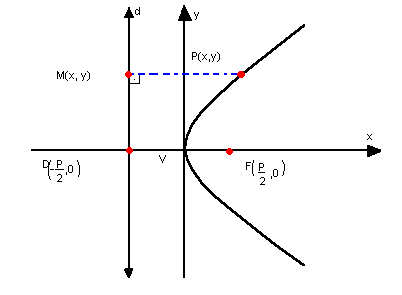
    Como a reta d tem equação 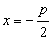  e na parábola temos:

• ;
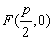• P(x, y);
• d_PF = d_Pd ( definição);

        obtemos, então, a equação da parábola:

y2 = 2px

b) parábola com vértice na origem, concavidade para a esquerda e eixo de simetria horizontal

Nessas condições, a equação da parábola é:

y2 = -2px

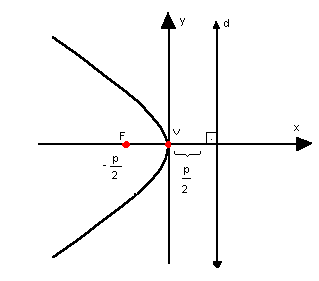c) parábola com vértice na origem, concavidade para cima e eixo de simetria vertical

x2=2py

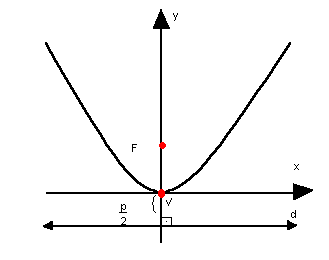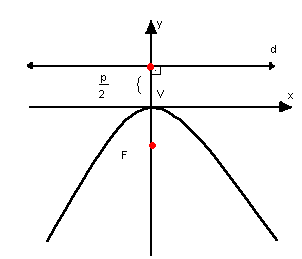
d) parábola com vértice na origem, concavidade para baixo e eixo de simetria vertical

x2= - 2py