Desenvolvendo a superfície lateral de um cone circular reto, obtemos um setor circular de raio g e comprimento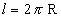 
:
:
Assim, temos de considerar as seguintes áreas:
a) área lateral (AL): área do setor circular
b) área da base (AB):área do circulo do raio R
c) área total (AT):soma da área lateral com a área da base
Volume
Para determinar o volume do cone, vamos ver como calcular volumes de sólidos de revolução. Observe a figura:
 |
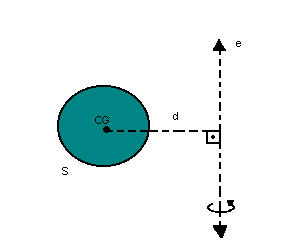d = distância do centro de gravidade (CG) da sua superfície ao eixo e
S=área da superfície
|
Sabemos, pelo Teorema de Pappus - Guldin, que, quando uma superfície gira em torno de um eixo e, gera um volume tal que:
Vamos, então, determinar o volume do cone de revolução gerado pela rotação de um triângulo retângulo em torno do cateto h:
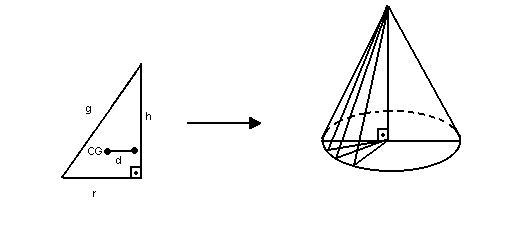
O CG do triângulo está a uma distância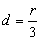 
do eixo de rotação. Logo:
do eixo de rotação. Logo:
Nenhum comentário:
Postar um comentário