Retas: Equações paramétricas

   São equações equivalentes à equação geral da reta, da forma x= f(t) e y= g(t), que relacionam as coordenadas x e y dos pontos da reta com um parâmetro t.

   Assim, por exemplo, 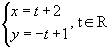, são equações paramétricas de uma reta r.

   Para obter a equação geral dessa reta a partir das paramétricas, basta eliminar o parâmetro t das duas equações:

 x = t + 2 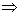t = x -2

   Substituindo esse valor em y = - t + 1, temos:

y = -(x - 2) + 1 = -x + 3 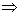 x + y - 3 = 0  ( equação geral de r)

Equação Reduzida

   Considere uma reta r não-paralela ao eixo Oy:

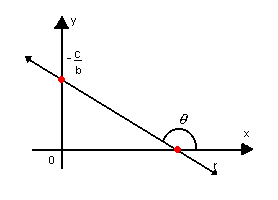
   Isolando y na equação geral ax + by + c = 0, temos:

    Fazendo 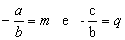, vem:

y = mx + q

   Chamada equação reduzida da reta, em que 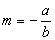 fornece a inclinação da reta em relação ao eixoOx.

   Quando a reta for paralela ao eixo Oy, não existe a equação na forma reduzida.