Chamamos de coeficiente angular da reta r o número real m tal que:
O ângulo 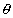 é orientado no sentido anti-horário e obtido a partir do semi-eixo positivo Ox até a reta r. Desse modo, temos sempre
é orientado no sentido anti-horário e obtido a partir do semi-eixo positivo Ox até a reta r. Desse modo, temos sempre 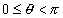 .
.
Assim:
- para
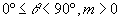 ( a tangente é positiva no 1º quadrante)
( a tangente é positiva no 1º quadrante) - para
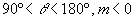 ( a tangente é negativa no 2º quadrante)
( a tangente é negativa no 2º quadrante)
Exemplos:
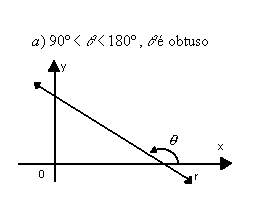
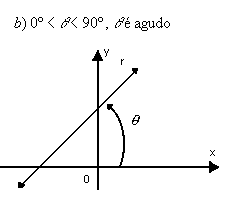
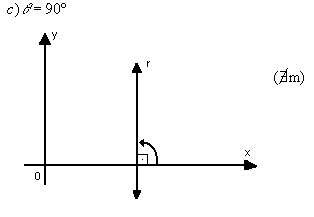
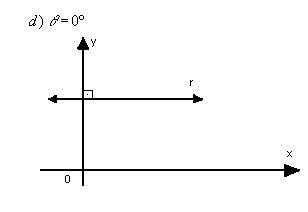
Determinação do coeficiente angular
Vamos considerar três casos:
a) o ângulo 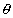 é conhecido
é conhecido
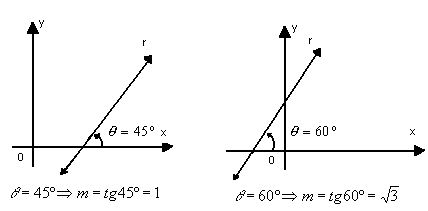
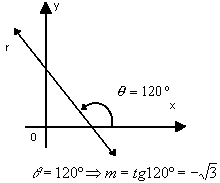
b) as coordenadas de dois pontos distintos da reta são conhecidas: A(xA, yA) e B(xB, yB)
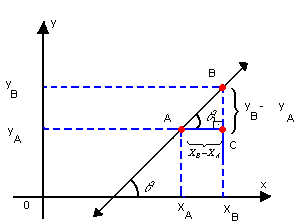 |
Como 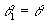 ( ângulos correspondentes) temos que
( ângulos correspondentes) temos que 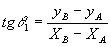 .
.
Mas, m = tg 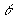 Então:
Então:
Assim, o coeficiente angular da reta que passa, por exemplo, por A(2, -3) e B(-2, 5) é:
c) a equação geral da reta é conhecida
Se uma reta passa por dois pontos distintos A(XA, YA) e B(XB, YB), temos:
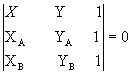
Aplicando o Teorema de Laplace na 1ª linha, vem:
(YA - YB)x + (XB - XA)y + XAYA - XBYB = 0
Da equação geral da reta, temos:
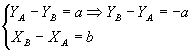
Substituindo esses valores em 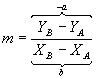 , temos:
, temos:
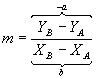 , temos:
, temos:
Nenhum comentário:
Postar um comentário