Se três pontos, A(xA, yA), B(xB, yB) e C(xC, yC), estão alinhados, então:
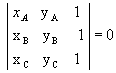
Para demonstrar esse teorema podemos considerar três casos:
a) três pontos alinhados horizontalmente
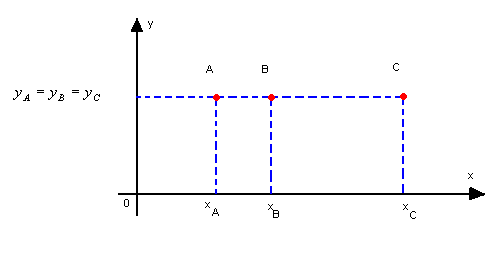
Neste caso, as ordenadas são iguais:
yA = yB = yC
e o determinante é nulo, pois a 2ª e a 3ª coluna são proporcionais.
b) três pontos alinhados verticalmente
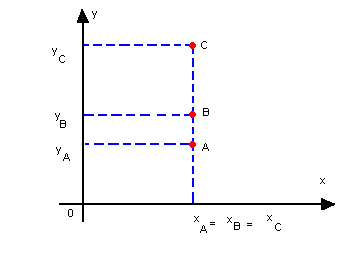
Neste caso, as abscissas são iguais:
xA = xB = xC
e o determinante é nulo, pois a 1ª e a 3ª coluna são proporcionais.
c) três pontos numa reta não-paralela aos eixos
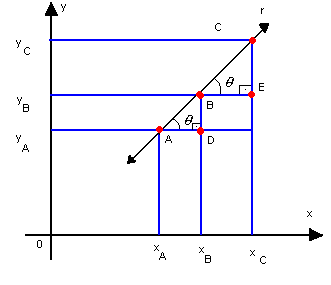
Pela figura, verificamos que os triângulos ABD e BCE são semelhantes. Então:
Desenvolvendo, vem:
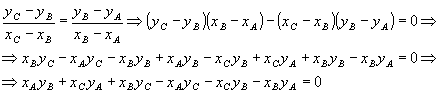
Como:
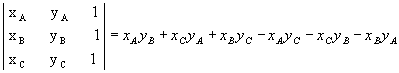
então 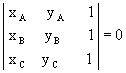 .
.
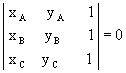 .
.
Observação: A recíproca da afirmação demonstrada é válida, ou seja, se 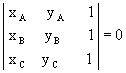 , então os pontos A(xA,yA), B(xB,yB) e C(xC, yC) estão alinhados.
, então os pontos A(xA,yA), B(xB,yB) e C(xC, yC) estão alinhados.
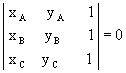 , então os pontos A(xA,yA), B(xB,yB) e C(xC, yC) estão alinhados.
, então os pontos A(xA,yA), B(xB,yB) e C(xC, yC) estão alinhados.
Nenhum comentário:
Postar um comentário