Retas:Ponto médio

   Dados os pontos A(x_A, y_A), B(x_B, y_B) e P,  que divide 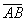 ao meio, temos:

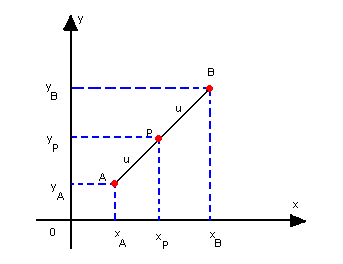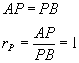Assim:

Logo, as coordenadas do ponto médio são dadas por:

Baricentro de um triângulo

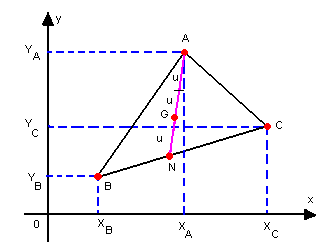
   Observe o triângulo da figura a seguir, em que M, N e P são os pontos médios dos lados 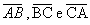, respectivamente. Portanto,  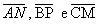são as medianas desse triângulo:

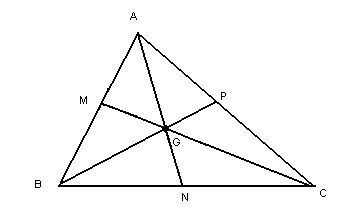
    Chamamos de baricentro (G) o ponto de intersecção das medianas de um triângulo.

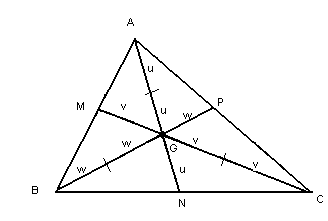
   Esse ponto divide a mediana relativa a um lado em duas partes: a que vai do vértice até o baricentro tem o dobro da mediana da que vai do baricentro até o ponto médio do lado.

Veja:

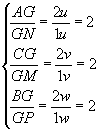Cálculo das coordenadas do baricentro

   Sendo A(X_A, Y_A), B(X_B, Y_B) e C(X_C, Y_C) vértices de um triângulo, se N é ponto médio de , temos:

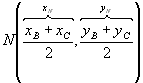Mas:

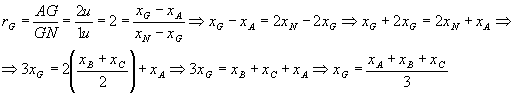
Analogamente, determinamos 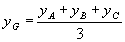. Assim: