SEQUÊNCIAS
Definição: Uma sequência é uma função cujo domínio é o conjunto dos números inteiros positivos. O contradomínio de uma sequência será considerado o conjunto dos números reais.
A cada número inteiro positivo "n" corresponde um número real f(n).
a1 = f(1) ; a2 = f(2) ; a3 = f(3) ; ... ; an = f(n)
Notações:
{an} = {a1, a2, a3, ..., an, ...}
an é o termo genérico da sequência.
Exemplos:
1) 
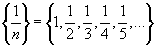
2) 
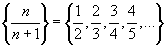
Se, quando n cresce, an se torna cada vez mais próximo de um número real L, diz-se que a sequência {an} tem limite L (ou converge para L) e se escreve:
Uma sequência que não é convergente, é chamada de divergente.
TEOREMA DO SANDUÍCHE
Se {an}, {bn}, {cn} são sequências tais que an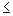
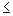bn cn para todo 
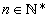e se
Se {an}, {bn}, {cn} são sequências tais que an
bn cn para todo e se
então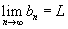 
SÉRIES
Definição: Se {an} é uma sequência, então:
A soma infinita a1 + a2 + a3 + ... + an + ... =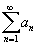 
é chamada série.
é chamada série.
Cada número ai é um termo da série;
an é o termo genérico de ordem n.
Para definir a SOMA de infinitas parcelas, consideram-se as SOMAS PARCIAIS.
S1 = a1
S2 = a1 + a2
S3 = a1 + a2 + a3
------------------------
Sn = a1 + a2 + a3 + ... + an-1 + an
E a SEQUÊNCIA DAS SOMAS PARCIAIS
S1, S2, S3, ..., Sn, ...
Se essa sequência tem limite S, então a série CONVERGE e sua soma é S.
Ou seja: Se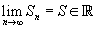 
, então a série converge e sua soma é a1+a2+a3+...+an... = S
, então a série converge e sua soma é a1+a2+a3+...+an... = S
Se a sequência {Sn} não tem limite, então a série DIVERGE.
Nenhum comentário:
Postar um comentário