Hipérbole eqüilátera

Hipérbole eqüilátera

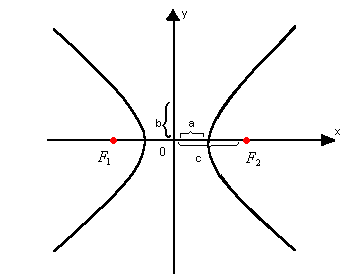
    Uma hipérbole é chamada eqüilátera quando as medidas dos semi-eixos real e imaginário são iguais:

a = b

Assíntotas da hipérbole

    Assíntotas são retas que contêm as diagonais do retângulo de lados 2a e 2b.

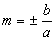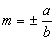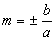    Quando o eixo real é horizontal, o coeficiente angular dessas retas é ; quando é vertical, o coeficiente é .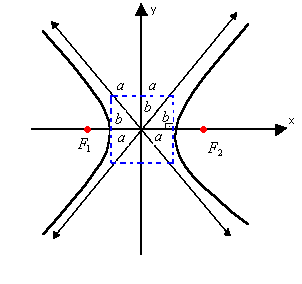

Equação

    Vamos considerar os seguintes casos:

a) eixo real horizontal e C(0, 0)

    As assíntotas passam pela origem e têm coeficiente angular 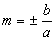; logo, suas equações são da forma:

b) eixo vertical e C(0, 0)

    As assíntotas passam pela origem e têm coeficiente angular 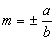; logo, suas equações são da forma:

Parábola

    Dados uma reta d e um ponto F 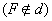, de um plano 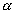, chamamos de parábola o conjunto de pontos do plano  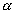eqüidistantes de F e d.

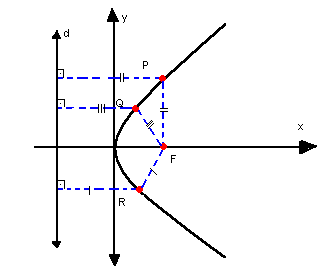
   Assim, sendo, por exemplo, F, P, Q e R pontos de um plano 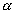 e d uma reta desse mesmo plano, de modo que nenhum ponto pertença a d, temos:

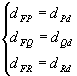Observações:

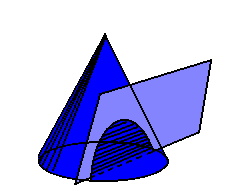
1ª) A parábola é obtida seccionando-se obliquamente um cone circular reto:

2ª) Os telescópios refletores mais simples têm espelhos com secções planas parabólicas.

3ª) As trajetórias de alguns cometas são parábolas, sendo que o Sol ocupa o foco.

4ª) A superfície de um líquido contido em um cilindro que gira em torno de seu eixo com velocidade constante é parabólica.