SÉRIES DE POTÊNCIA

SÉRIE-P

    

CONVERGE se p > 1

DIVERGE se p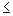1

Se p = 1, a série

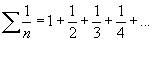é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente.

SÉRIE ALTERNADA

É da forma:

SÉRIES DE POTÊNCIA

Séries de potências de x:

ou

Séries de potência de (x-c):

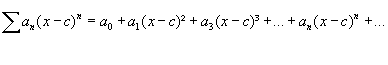
Por conveniência, vamos admitir que 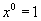, mesmo quando x = 0.

Ao substituir x por um número real, obtém-se uma série de termos constantes que pode convergir ou divergir.

Em qualquer série de potências de x, a série converge sempre para x=0, pois se substituirmos x por0 a série se reduz a a₀.

Na série de potências de (x-c), a série converge para x = c.

Para determinar os outros valores de x para os quais a série converge, utiliza-se o teste da razão.

TESTE DE LEIBINZ

Uma série alternada CONVERGE se:

* Seu termo genérico, em módulo, tende a zero.

* A série dos módulos é decrescente.

Há três maneiras diferentes de verificar se a série dos módulos é decrescente.

a) verificar se, para todo "k" inteiro positivo, .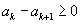

b) verificar se, para todo "k" inteiro positivo, .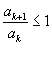

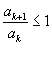c) considerar a função f(x) = f(n) e verificar o sinal de sua derivada. Se f'(x)<0, então f é decrescente.